Taproot is a soft fork of the Bitcoin network which led to the creation of several Bitcoin Improvement Proposals (BIPs), the most notable being BIP 340 and BIP 341. Given that scalability is a challenge, efficiency and privacy have long been at the center of the Bitcoin community, and layer two technologies like the Lightning network have helped in this regard. With the introduction of taproot, the bitcoin network can scale more efficiently. An excerpt from Bitcoin magazine comments on the Bitcoin's Taproot upgrade: "Security is the lifeblood of every Bitcoiner. Unwilling to shake their core beliefs of hard, sound money, the Bitcoin community paced themselves to make sure the Layer 1 (Bitcoin protocol) was immutable, efficient, and proven to be 100% secure before "upgrading."

Spending coins which have been sent to a Taproot address requires either fulfilling one of the committed scripts or just supplying a signature that can be verified against the public key (allowing the script to be kept private). Taproot employs the use of Schnorr signatures and an updated script that allows the scripting language to use Schnorr signatures and Merkelized Abstract Syntax Trees (MAST). Taproot also introduces Tapscript, an update to the bitcoin scripting language: substituting some operations, enabling some previously-disabled operations and using a different signature calculation for sighashes.

I will describe the BIPs and principles of Taproot in a three-part series with an emphasis on:

1. Schnorr signatures using secp256k1, BIP 340
2. Merkelized Abstract Syntax Trees (MAST) BIP 114 and,
3. Taproot BIP 341.

The two articles that follow will be on MAST and the conglomerate Taproot, but let's start with Schnorr signatures first.

SCHNORR SIGNATURES

The concept of Schnorr signatures is proof of knowledge of a private key. In Bitcoin, this means that coin owners prove ownership by using signatures, which is already achievable with the current implementation of the Elliptic Curve Signature Derivation Algorithm (ECDSA). However, Schnorr signatures are a substitute for ECDSA that introduces several fascinating modifications to Bitcoin, some of which include:

• improved privacy, especially with multi-signature transactions,
• aggregation of multiple signatures into one signature,
• introduces adaptor signatures—signatures that, when satisfied, reveal the real signatures,
• atomic swaps between different chains,
• more block space due to reduced transaction size,
• you may optionally commit to a script that can be revealed at spend time.

Let's first comprehend the creation of Schnorr signatures before making a practical comparison to how it is applied in a bitcoin transaction using Alice and Bob, two well-known characters.

Steps

1.) Ingredients of Schnorr signatures

• Choose a generator point, G which in Bitcoin is from an elliptic curve (EC) (secp256k1 curve). The elliptic curve is made up of a group of prime field numbers Fp of order p, where p is a prime number.

The prime field F of order p can be described as follows: Say you have a prime number 7 and you choose elements 5 and 6; to derive their sum, you would perform the following computation: 5 + 6 = 11 modulo 7; Since the addition of 5 and 6 is greater than the prime number 7, we derive the modulus (remainder) by dividing the sum 11 by the prime number 7. Hence, our result is 5 + 6 = 4 and that is how we derive our prime field. Keep in mind that this is modular arithmetic, which is commonly used in cryptography.

• Next, choose a Schnorr group of numbers, which is basically a large but finite set of prime field numbers of prime order.

• Choose a cryptographic hash function, Ha e.g. sha256.

However, some things to note are: multiplying the scalar with the generator point, G, means, adding G to itself, a scalar number of times. e.g. a.G = (G + G + G + ... + G)

2.) Key generation

• Choose a private key x for signing messages (Bitcoin transactions). In this case, x is referred to as a scalar which is an element of the prime field Fp.

• Derive the public key P from the private key by multiplication of x * G = P.

x.G represents a point {x, y} on the bitcoin elliptic curve. The public key P, can later be used to derive Bitcoin addresses.

3.) Generating a signature to sign transaction

• To sign a transaction, T, choose a nonce, k which is a random number we use only once, for this transaction.
• We create a random point R, by multiplying k * G.
• We then implement a hashing algorithm on our nonce and transaction r = Ha(R, T). Hashing the transaction with the random point now commits to the transaction, which is needed for others to verify the signature and so that the signature for one transaction can't be used for another transaction. The hash function will be used on each transaction primarily to make the protocol non-interactive.
• Next, we derive a signature equation s = k + (x.r).
• This gives us a signature pair S = (s, r) for our public key, which we can use to sign and verify transactions.

However, we need to ensure our signature is verifiable by others without necessarily giving them our private key. For anyone to validate the transaction, the verification method must be made non-interactive. This is an important aspect of Bitcoin because signature verification is essential to proving ownership and spending of your coins. Verifying a Schnorr signature is relatively easy.

• We basically apply and multiply our signature equation s = k + (x.r) with the fixed generator point.
• This gives us s*G = k*G + (x*G)(r)

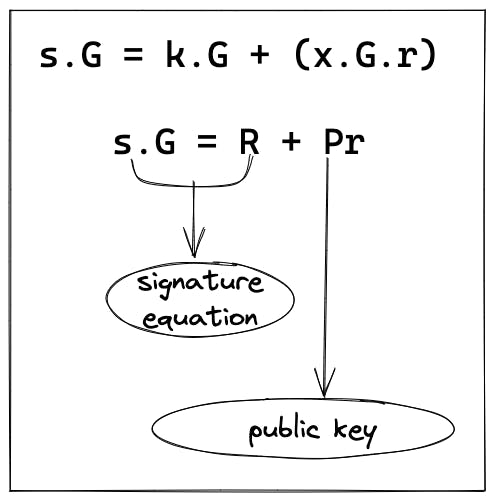
From the figure above, you'd notice the public key and signature is publicly known, the generator point G is always fixed in Bitcoin, and the hash r is publicly known because it always produces the same hash.

That is a significant amount of high school math. Using the pictorial illustration below as a reference, let's put this into practice by doing a Bitcoin transaction from Alice to Bob.

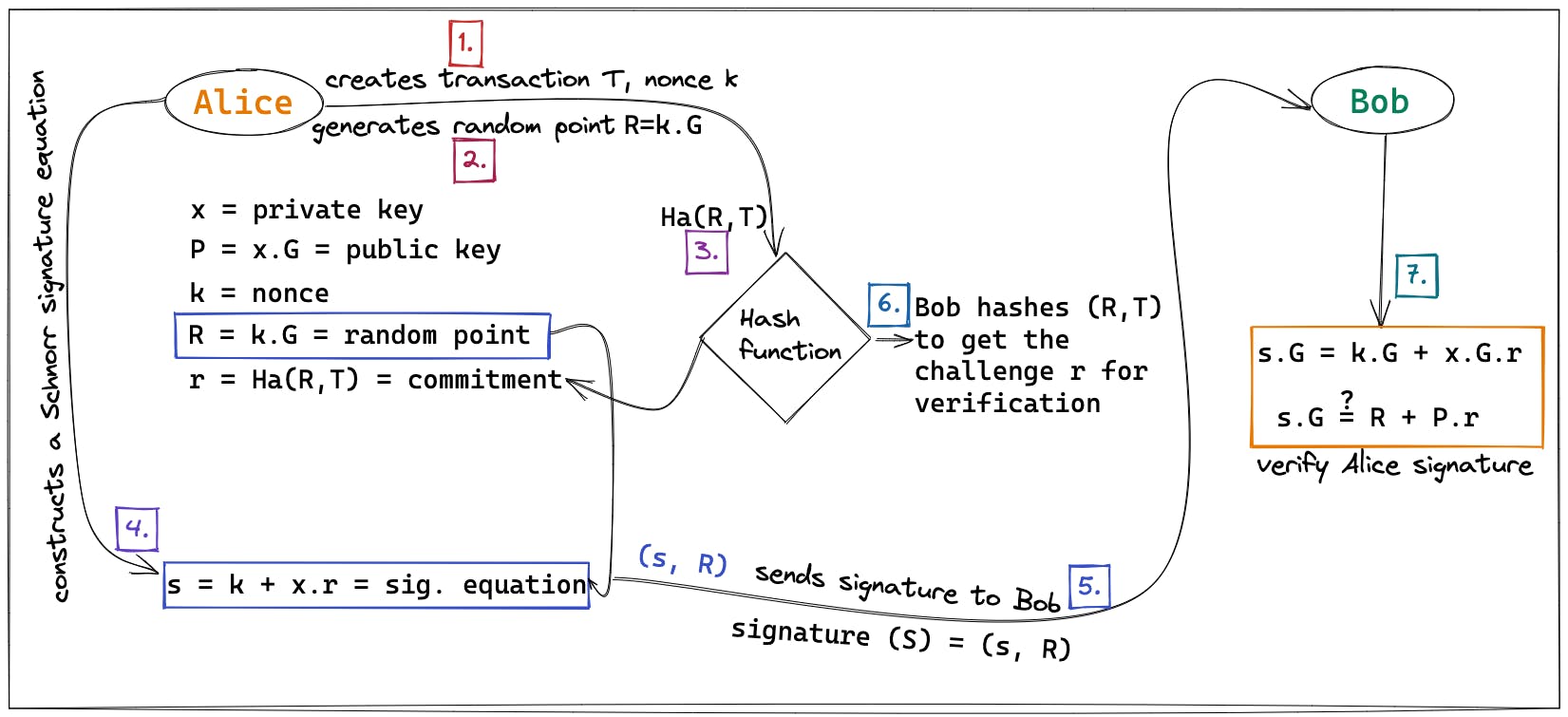
• Alice creates a transaction spending from her wallet using her private key x and public key P.
• To create a signature for that transaction T, she chooses a random nonce k and converts it to a public point R.
• She then passes the public point and the transaction into a hash function Ha(R,T) to make the signature unique to that transaction only. Hence, we derive a sort of commitment r.
• She also creates a signature equation s using the nonce, the commitment, and the private key.
• Now she has the building blocks to construct a Schnorr signature S which is the combination of the signature equation s and the random point R which she sends to Bob along with the transaction.
• On receiving the transaction, Bob has to verify that Alice has ownership of the elements in the transaction by checking the validity of the signature since he doesn't have Alice's private key.
• Bob first hashes the random point (which he got from the signature) and the transaction message to derive the same transaction commitment r.
• Next, he uses the fixed generator point G to compute the signature equation s. If the signature equation is valid, then Alice's signature is valid.

Conclusion

Schnorr signatures are simpler and easier to verify than the ECDSA. However, due to standardisation and patent issues, it was not effectively used until recently. These standardisation issues have been covered in the BIP 340 which added a number of improvements not specific to Schnorr signatures. The Most notable of them are:

• The DER-encoding of variable size up to 72 bytes used for the signature encoding approach was replaced to a straightforward fixed 64-byte format.
• Public keys in this proposal are encoded as 32 bytes rather than the current practice in Bitcoin, which uses compressed 33-byte encodings of elliptic curve points.
• Compared to ECDSA, which requires additional witness data for batching, batch transaction verification is simpler.

The future prospects for Schnorr signatures are endless. As Bitcoin developers continue to explore Taproot and integrate it with wallets, we expect the network to scale efficiently.

In the next article, we will consider the update to Bitcoin Script and how it accommodates Schnorr signatures using Merkelized Abstract Syntax Trees (MAST).

References

• Banner image: Photo by Karolina Grabowska: pexels.com/photo/close-up-shot-of-a-bitcoin..

• bitcoinmagazine.com/technical/understanding..

• bitcoinops.org/en/topics/taproot

• academy.binance.com/en/articles/what-do-sch..

• cryptobook.nakov.com/digital-signatures